Hi folks! It's been a long time without posting anything here. I don't know if you saw my last update but recently I joined ConsenSys as a Blockchain Protocol Engineer.
I'm new to this whole Blockchain world and I've been learning lots of things in the past weeks. I'm really excited about this new challenge and I'm having a lot of fun in the process.
The idea for this post started when I started to invest some time to read Ethereum's White Paper and Yellow Paper. Briefly, this is what happened to me:
- I read the White Paper and realised how much I wanted to learn more about Ethereum;
- Did a lot of research about Ethereum (blog posts, articles, tutorials, etc.);
- Started reading the Yellow Paper first pages and realised that I couldn't understand a thing about what I was reading;
- Started to freak out thinking how dumb I was!
After a few days of terror, and after talking with other people, it became clear that I wasn't the only one in that situation. And that's the goal of this post: do a walkthrough on the Ethereum Yellow Paper as I read it, step-by-step, trying to simplify some of the concepts and create a mental model of the main parts of the protocol.
(DISCLAIMER: if you already know about Ethereum and the protocol, this post is probably not useful for you. I'm using this as a platform to help myself learn and eventually help others learn more about the protocol - you've been notified!)
(DISCLAIMER 2: this post is based on the current version of the Yellow Paper, version b9ee254 from 2018-02-12)
So, let's get started!
Introduction
(This is the easy part! Don't get used to it!)
In this section, the authors talk about the goal of the Ethereum project, the driving factors of the project and also give a lot of references to previous works in the field.
Takeaways:
- Ethereum wants to create a new decentralised computer, where anyone would be able to be part of it and use it.
The Blockchain Paradigm
"Ethereum [...] can be viewed as a transaction-based state machine."
I come from a Computer Science background. I still remember when I studied the architecture of a computer system. Basically, the simplest definition of a computer that you can get will be something like this:
"'something' that is capable of getting some input, do some processing, store data, and give an output."
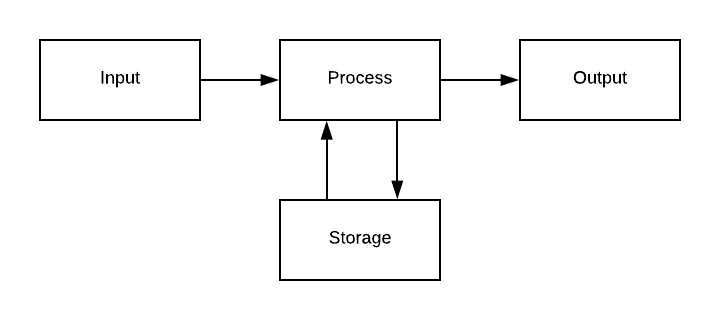
(If you want a not so simplistic definition, take a look at Von Neumann computer architecture.)
From a simplistic point of view, if you compare Ethereum model where transactions and smart contract executions change the state of a node, you can think about it as a computer. Therefore, if you replicate this logic in a number of nodes, distributed in a p2p network, and add a way for these nodes to agree on the order of operations executed and the correct state, you'll end up with a decentralised computer, where nodes perform calculations (process) using transactions (inputs), storing the results (storage) that can be queried later (output).
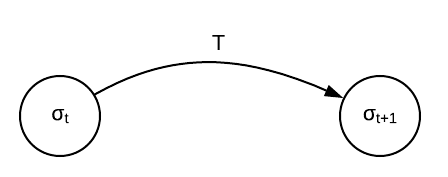
Equation number 1 is all about a mathematical definition of the "Ethereum computer" as a sequence of state transitions. Let's take a look:
$$\sigma_{t+1} \equiv \Upsilon (\sigma_t, T) \tag{1}$$
In this formula, we have the following members:
- $\sigma_{t+1}$ is the next world state (more about world state later)
- $\Upsilon$ is the Ethereum state transition function
- $\sigma_{t}$ is the current world state
- $T$ is a transaction
All this equation is saying is that a transaction (input) affects (process) the current world state (storage) and as result, we have the new world state (storage/output).
Another way of thinking about it is as a state transition machine. In this model, a transaction $T$ is the arc between the current state $\sigma_{t}$ and the next state $\sigma_{t+1}$.
(We'll talk more about Ethereum's world state in the following posts. If you want to learn more about it, you should check this blog post from Timothy McCallum.)
Expanding the model
In Ethereum, transactions are aggregated in blocks. And these blocks are chained together to form a blockchain. New blocks are added to the chain in a process called mining. The important thing to understand about the block generation process is that it requires computing power and electricity from the node that is creating it. Therefore, we need a mechanism to incentivise people to engage on this. Every time a node creates a new block, they get a reward.
So, we can expand the previous representation of Ethereum paradigm to include the blocks and the reward. And that's what the authors do in equations 2, 3 and 4. Let's take a look:
$$B \equiv (..., (T_0, T_1, ...)) \tag{3}$$
This equation represents a block as a list of transactions (and a few more things that we will omit for simplicity).
As we already know, we don't process transactions individually to update the world state. Therefore, we can rewrite the equation that represents the paradigm as the following:
$$\sigma_{t+1} \equiv \Pi(\sigma_t, B) \tag{2}$$
- $\sigma_{t+1}$ is the next world state
- $\Pi$ is the block-level state transition function
- $\sigma_{t}$ is the current world state
- $B$ is a block (list of some transactions)
In plain English, this equation is saying that the world state will be updated by applying the transactions from a block into the current state, producing a new state.
Last but not least, there is equation number (4). This equation consolidates everything that we talked about earlier in one single model:
$$\Pi(\sigma, B) \equiv \Omega(B, \Upsilon(\Upsilon(\sigma, T_0), T_1)...) \tag{4}$$
I know! It looks like an ugly equation and it seems that it doesn't make any sense. But all this is saying is that:
- When a block ($B$) is mined, the transactions ($T_0, T_1, ...$) are applied in sequence, and the output of each one of these functions ($\sigma$) is used as input for the next one.
- $\Omega$ is called block-finalisation state transition function and is a function that rewards a party.
To summarise, equation 4 states the way that a blockchain works. A node mines a block, the transactions on that block are applied (in sequence) on the world state, modifying it. Also, the node that mined the block gets a reward.
I know, it looks complicated. The first time I read it I also didn't understand anything. But relax, it's gonna get worse... :)
To finish this section, the author talks a little bit more about the reward that we saw before. Ethereum has its own currency (Ether) and this is the reward that nodes get from mining blocks. This currency can be divided into smaller parts, accordingly to this table:
| Multiplier | Name |
|---|---|
| $10^{0}$ | Wei |
| $10^{12}$ | Szabo |
| $10^{15}$ | Finney |
| $10^{18}$ | Ether |
Conclusion
Congratulations! If you read all the way here that means that you went through the first two pages of the yellow paper!
I hope that this helps you to understand the paper. I'm not used to academic papers and everything seemed impossible to grasp. But doing some research and reading it a thousand times helps. If this post helped you let me know, I'll be really happy!
I don't know when the next part is coming. I'll do my best to write about it as soon as I feel ready.
See you in the next one!
